上章节中我们讲解了如何神经网络如何学习权重以及梯度下降的原理及含义。本章节我们从数学的角度去解析梯度下降的推导方法。这个过程会涉及到神经网络的几个非常关键的参数如learning rate，gradient等。

我们已经知道，初始状态下我们的神经网络并不知道每一个输入的最佳权重，需要根据预测结果来调整权重参数。衡量误差的标准经常使用平方差SSE。

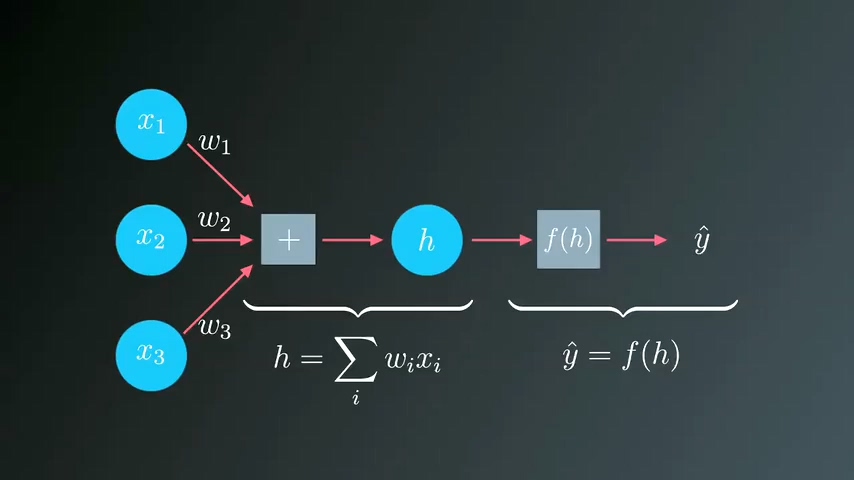
从上面公式可以看出，误差取决与权重值wi和xi，我们可以用矩阵来理解这个公式：

u=1代表第一行数据，X代表输入数据，y代表目标值。要计算整体误差，需要把每一行数据的误差进行累加。SSE数值越高，说明误差越大，预测效果越差。所以我们需要尽可能减小误差。下面举一个简单例子，用单个输入单行数据来表示。

单个输入单行数据的例子

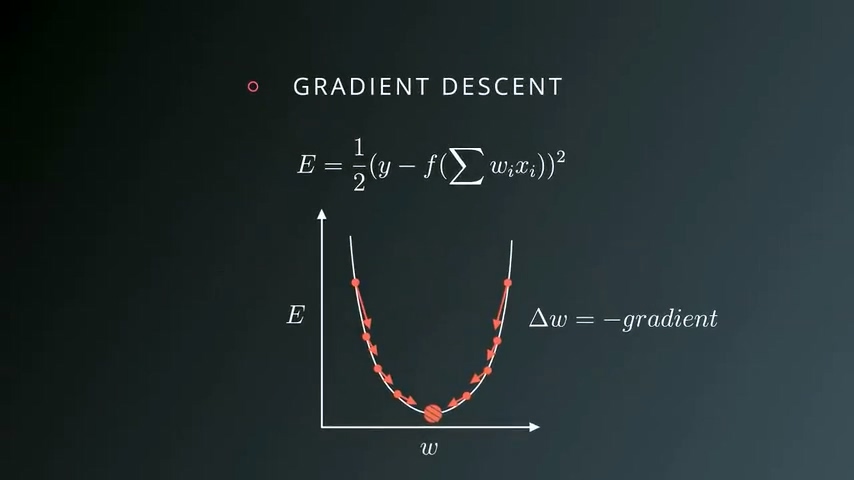
我们随机选取一个某个权重值，计算改点的梯度，寻找梯度下降的方向，每次修改Δw，直到某个权重使得梯度为0，也就是碗底的位置。

更新权重值

• wi’ 新的权重值
• wi 旧的权重值
• △wi 更新步长

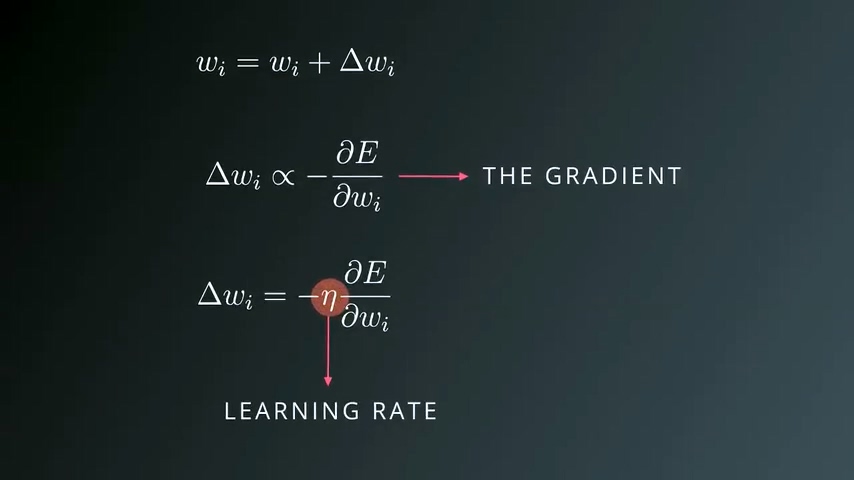
更新步长与梯度成正比关系，而梯度等于“误差关于每个权重值wi的偏导数”，公式中同时需要加入一个系数η，代表learning rate。

展开梯度公式

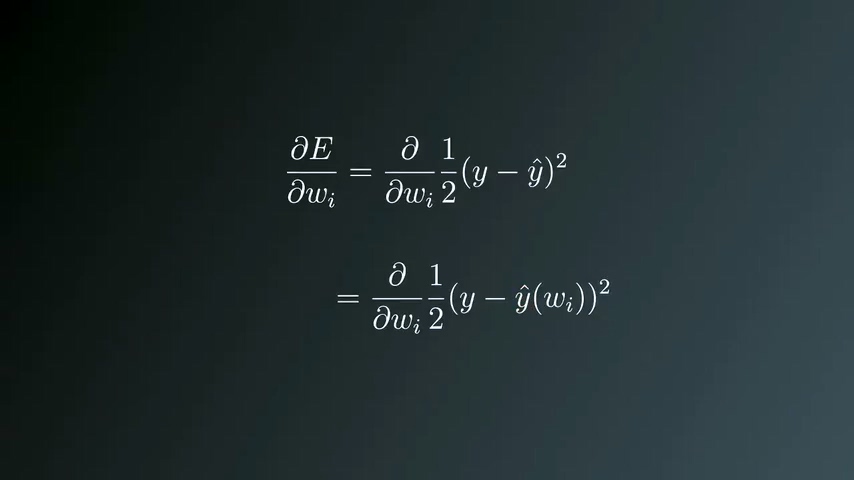
由于y是实数，求微分结果为0

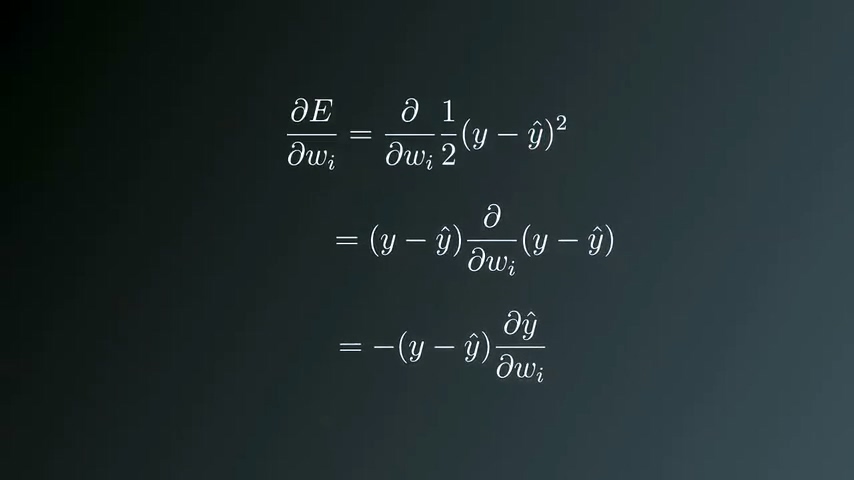
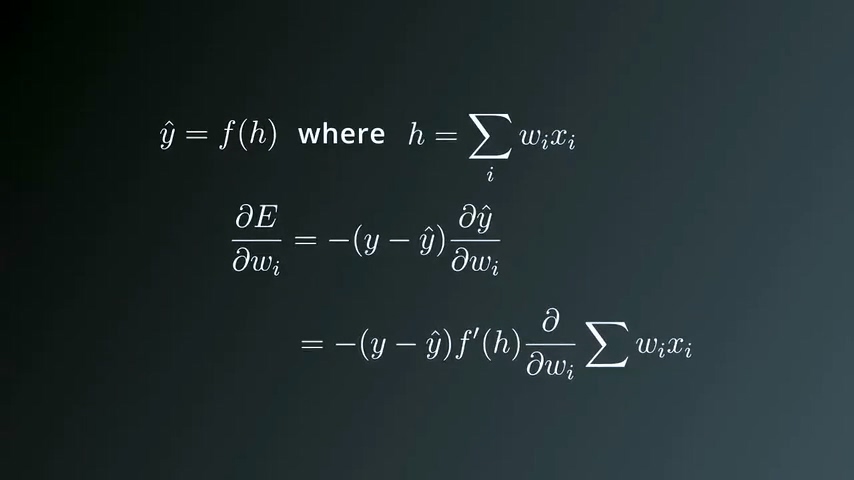
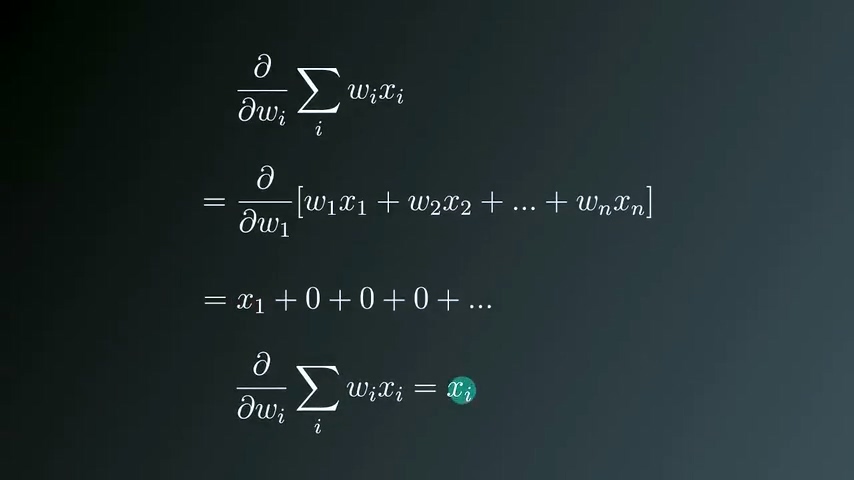
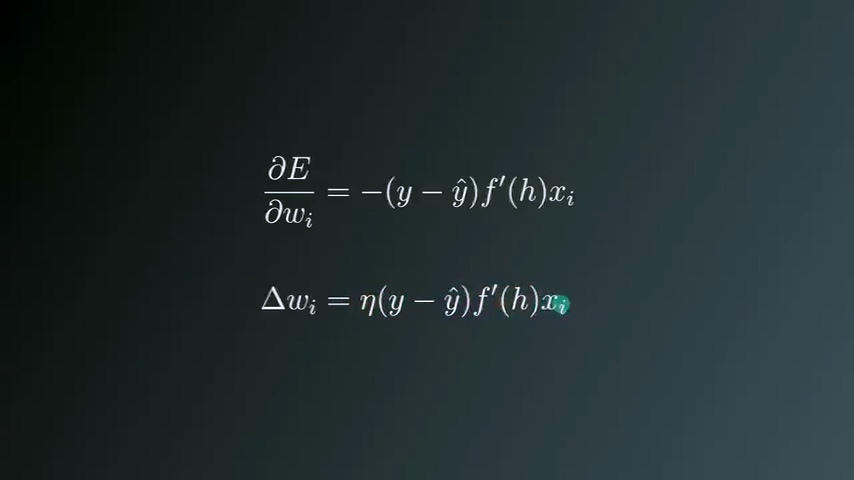
神经网络

神经网络可以视为单个输出网络的堆叠，所有输入都要连接到每一层的输入：

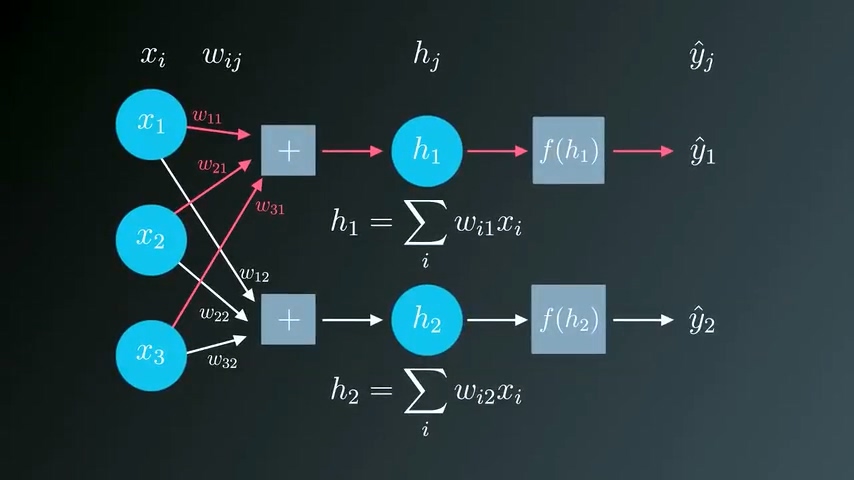
这时候整体的误差就等于每个输出单元的误差值之和。梯度下降法同样可以扩展适用于这种情况：

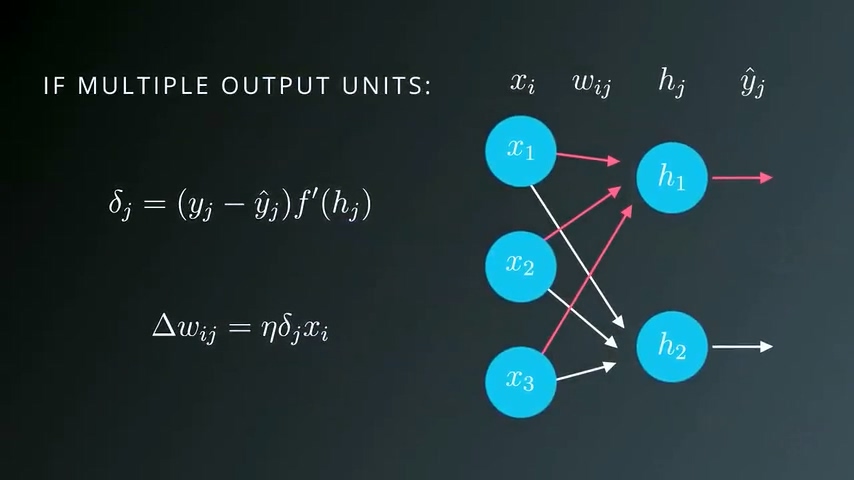
只需要分别计算每一个输出单元的误差项并求和，表示为δj