在上一章节感知器中我们学习了权重（weights）的概念，但是我们是手动设置各输入值的权重的。但很多时候我们并不知道每一个输入值真实的权重是多少，我们需要从现有的数据中学习权重，然后使用权重去做预测。

为了弄清我们如何找出各个权重，我们需要从最初的目标开始看。我们需要网络预测的值尽可能的接近真实值。为了度量，我们需要需要一个量纲来衡量预测值与实际值之间相差多少，这就是误差。常见的误差度量是平方差之和（SSE）。

这个公式中y’是预测值，而y是实际值。j是每个输入出值，u是所有数据点。

对于里面j的求和表示每个输出单元的真实值y与预测值y’的平方差并求和。外面的u求和表示所有数据点的预测平方差之和。这样就提供了所有数据点所有输出预测的总体错误情况。

平方差之和（SSE）是一个度量误差的不错选择，平方确保误差始终为正，并且较大的误差比较小的误差更容易受到惩罚，此外这个计算较为友好，只需要进行加法操作。

回顾一下神经网络的输出，预测值依赖于权重：

因此误差公式也可以表示为：

我们希望这个网络的预测误差越小越好，权重是我们可以用来实现这一目标的关键手段。我们通过找到权重Wij最小化平方误差E。为了使神经网络做到这一点，我们通常使用梯度下降法。

梯度下降

我们上一节其实提到过梯度下降，想象我们的误差是一座山峰，初始时我们位于山顶，需要找到一条最快到达山底的路径（最快减小误差）。每一步我们都应该选取最陡峭的也就是误差减小最快的方向，这就需要我们计算平方差的梯度。

梯度是变化率或者坡度的另一个术语。为了计算变化率，我们需要用到微积分，特别是微分。

f(X)的微分f(x)’返回的是f(x)在x点的坡度。举个例子：

f(X) = X^2

f(X)' = 2X

当X=2时，f(2)’=4

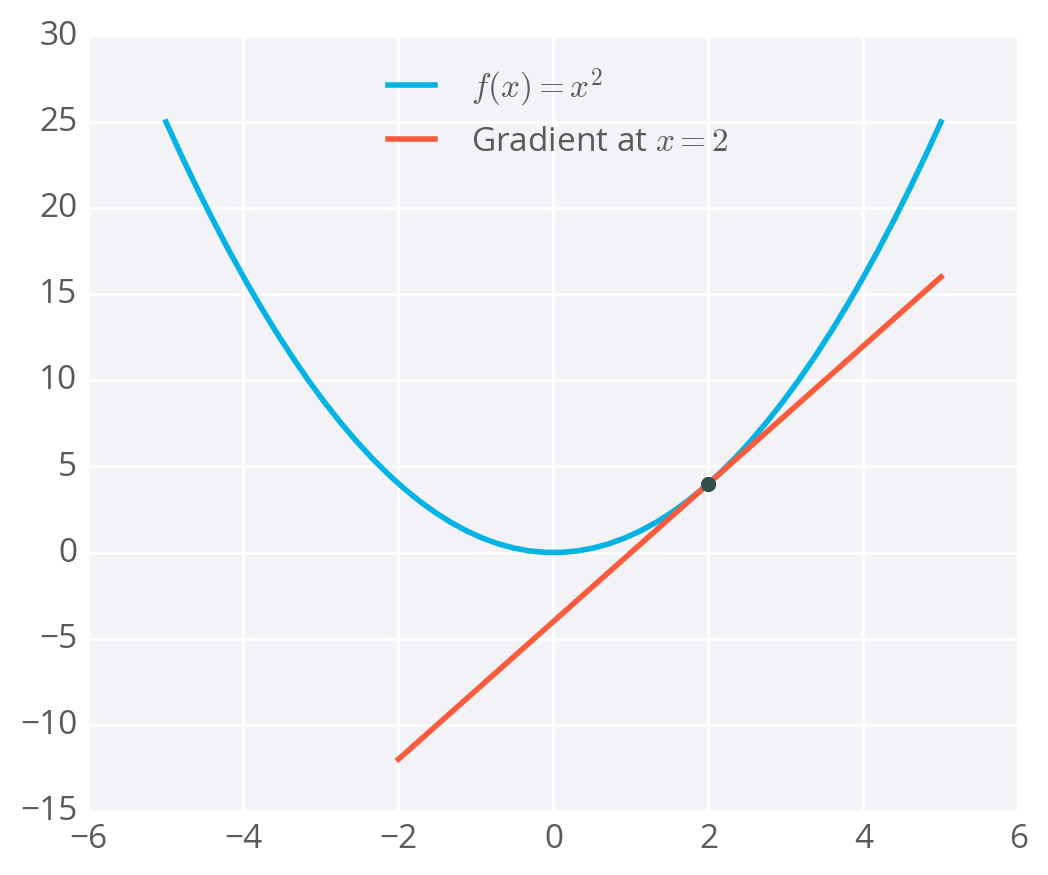
梯度只是导数，推广到具有多个变量的函数。我们可以使用微积分在我们的误差函数的任意点找到对应的梯度，下面我们将看到梯度下降的步骤。

梯度下降的步骤

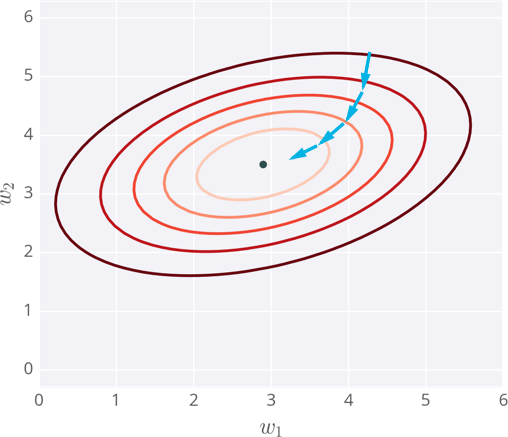
下图绘制了具有两个输入的神经网络误差的示例，因此图上有两个权重：W1和W2，你可以称之为等高线，每一条轮廓线上的点具有相同的误差。轮廓线颜色越深代表误差越大。每一个步骤中，我们计算误差和梯度，使用它们来确定修改每个权重的程度，重复这个过程最终找到接近误差函数最小值的权重即中间点。

因为权重会随着梯度下降的方向变化，权重最终可能达到一个误差较小的点，但可能不是最小的点。这些点称为局部最小值。如果使用了错误的初始权重值，则梯度下降法可以将权重引导到局部最小值。如下图所示：

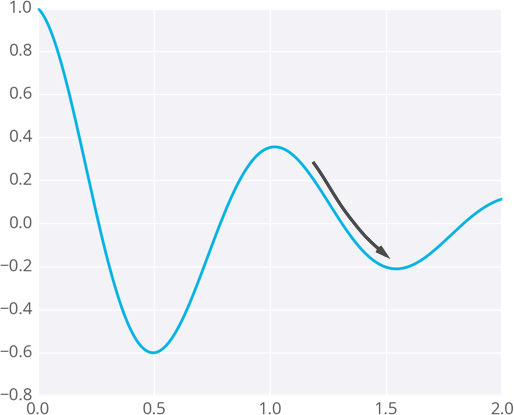
我们有一些方法是可以避免这个情况的，其中一种是动量法，下节我们将会讲到。