05-00 CNN–卷积神经网络简介
前面我们介绍的神经网络都是把全部数据输入进去然后进行学习的,这个过程会掺杂很多无用的信息使得学习过程非常低效。但是如果我们已经知道我们要识别或者学习的是什么,我们可以有更高效的方法进行神经网络的学习。
举个例子:如果我们要识别一些字母,这个字母的颜色并不影响识别的结果,那我们在将数据输入神经网络的时候是把彩色的数据全部输入进去还是只输入灰度信息呢?
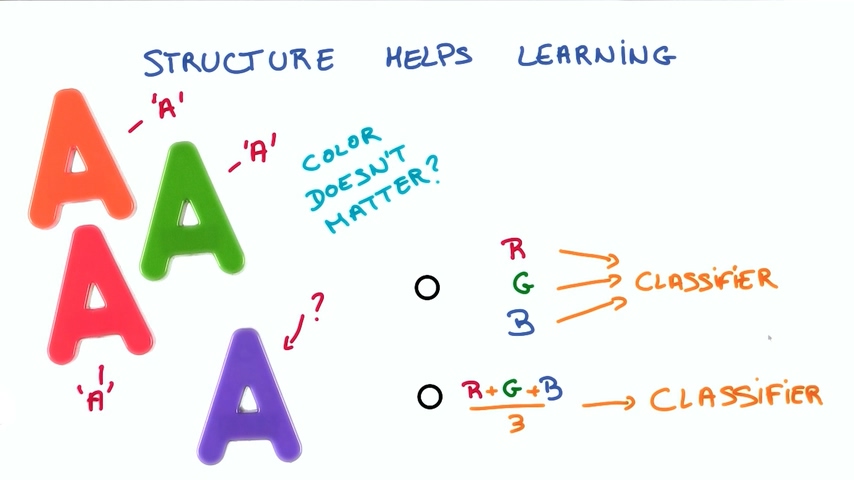
直观地说,如果有个字母的颜色是从来没有学习过的,那么忽略掉它的颜色将会使我们的神经网络更容易识别出这个字母到底是什么,所以只输入灰度信息是明智的做法。
统计不变性
平移不变性
第二个例子,我们有一张图片,我们希望神经网络可以识别出这是一张猫的图片,猫在图片中的哪个位置其实并不重要,它仍然是一张猫的图片。如果我们的神经网络需要识别出是在图片左下角有猫还是右上角有猫,那需要做的工作就要多得多。如果我们告诉神经网络,不管猫出现在图片的什么位置,对结果都没有影响,这就是是平移不变性

文本的例子
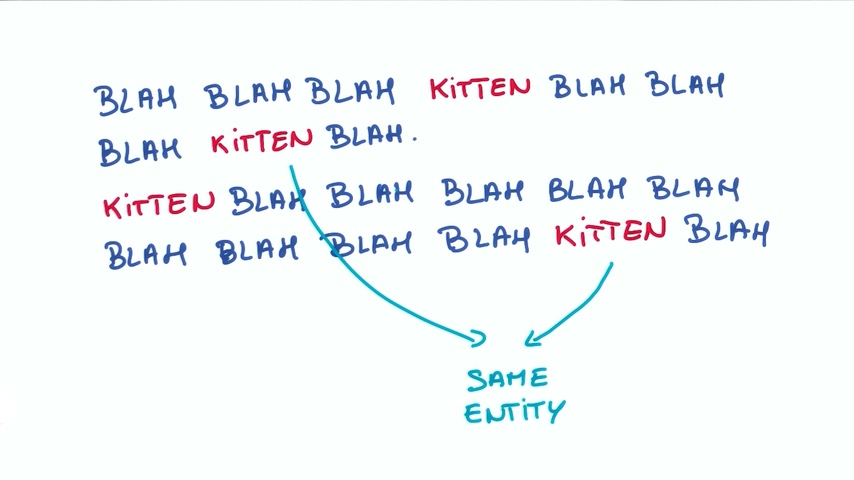
假设我们有一段话是关于猫咪(kitten)的,kitten这个词的含义会随着位置发生变化吗?比如在第一句和第二句中的kitten的含义有差别吗?大部分情况下并不会有什么不同。因此如果你尝试一个关于文本的网络,我们应该让神经网络学习到什么是kitten,并且可以重复使用,而不是每次遇到都要学习kitten是什么。
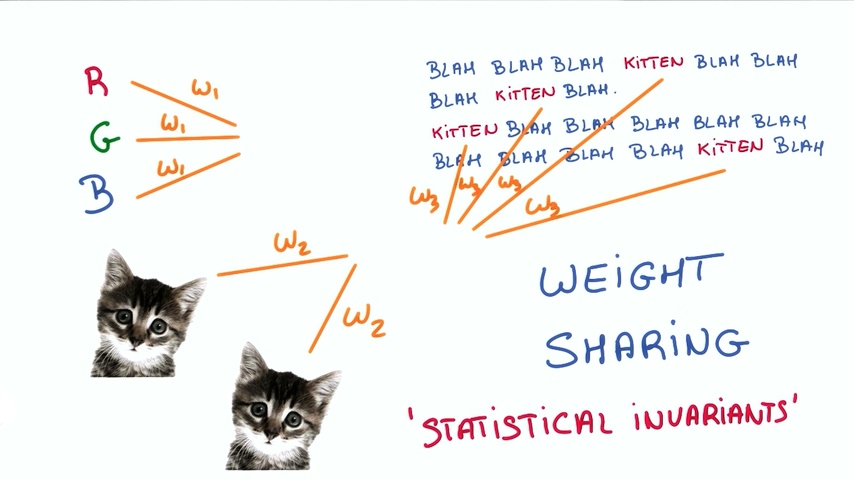
权重共享
实现这种不变性的方法叫做“权重共享”weight sharing。当我们知道两种不同的输入都会得到同一种结果,我们就经过共享权重并且利用这些输入共同训练权重。这就是统计不变性。事物的平均值并不随时间或者空间发生变化。对于图片来说,权重共享的思想使得我们去研究卷积神经网络(CNN Convolution Neural Networks);对于文本和序列,我们使用词嵌入和循环神经网络。
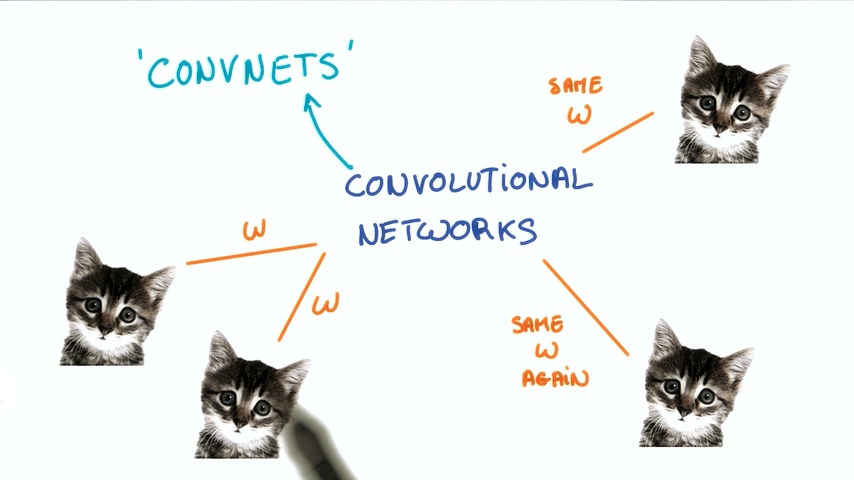
卷积神经网络
卷积神经网络(CNN Convolution Neural Networks)是一种在空间上共享参数的神经网络。
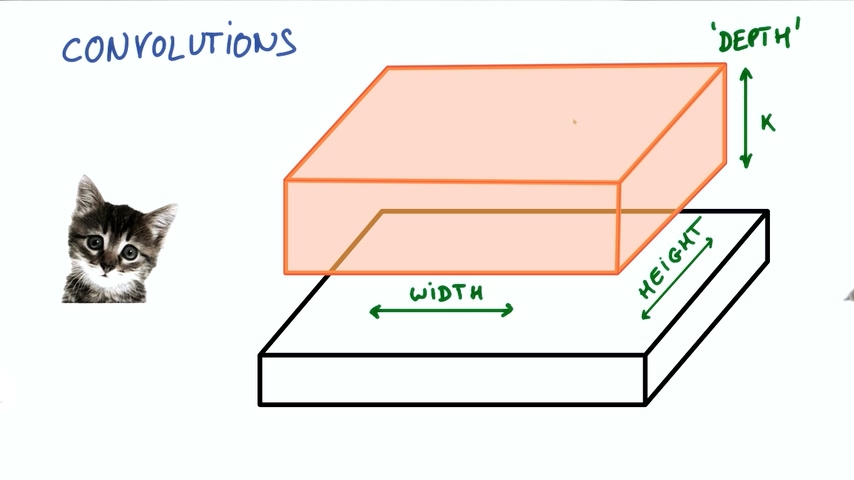
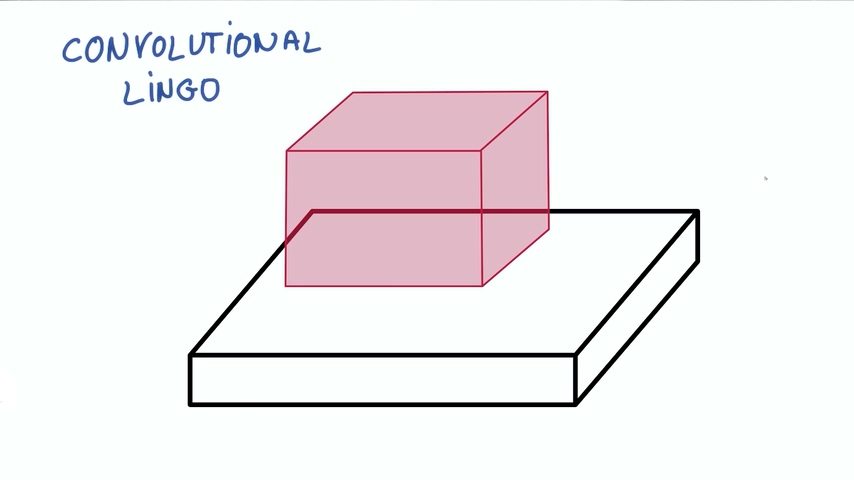
我们把图片想象成一个长方体,长和宽分别是像素点的数量,高是色彩RGB组合,也称为深度“DEPTH”。在下图的情况下深度为3.
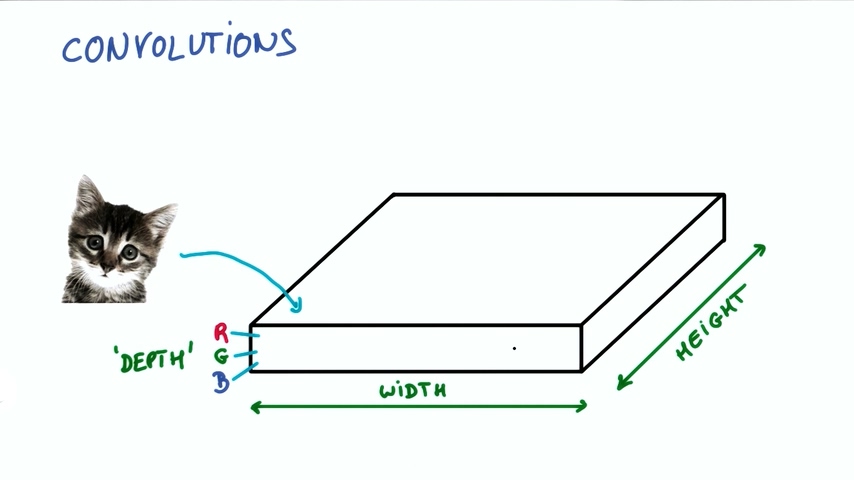
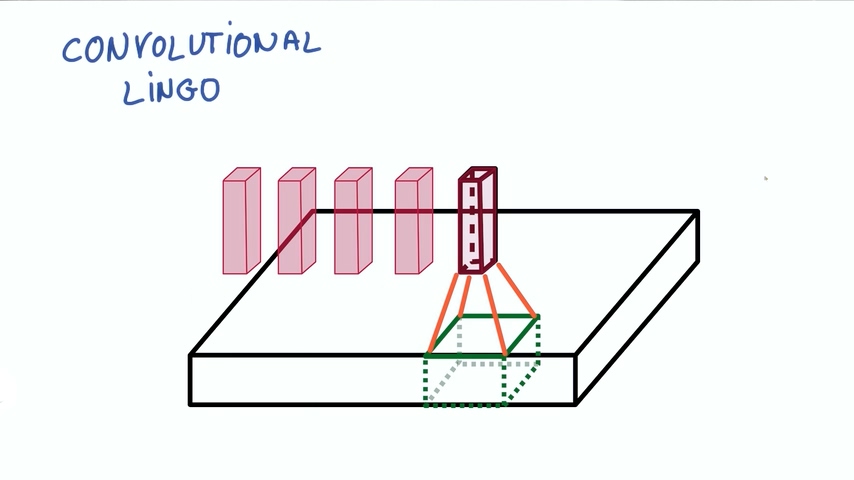
现在假设我们图片中取出一块,输入到一个有k个输出的小神经网络。
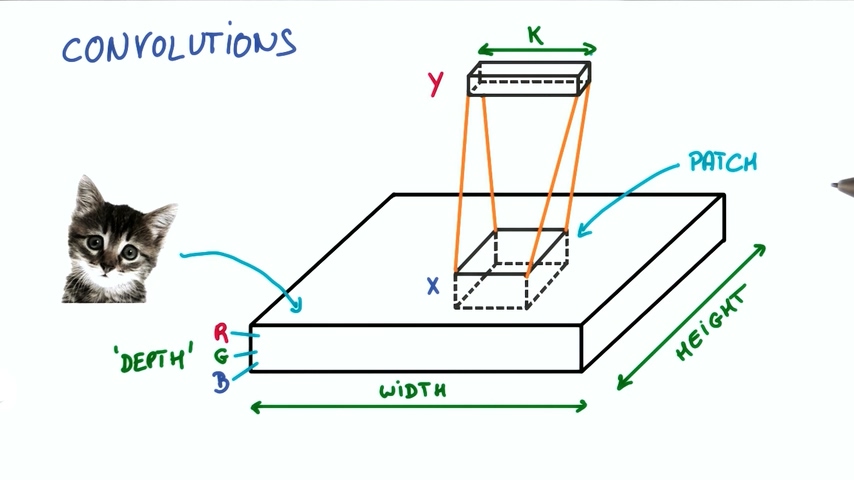
然后把输出表示为垂直的小列。
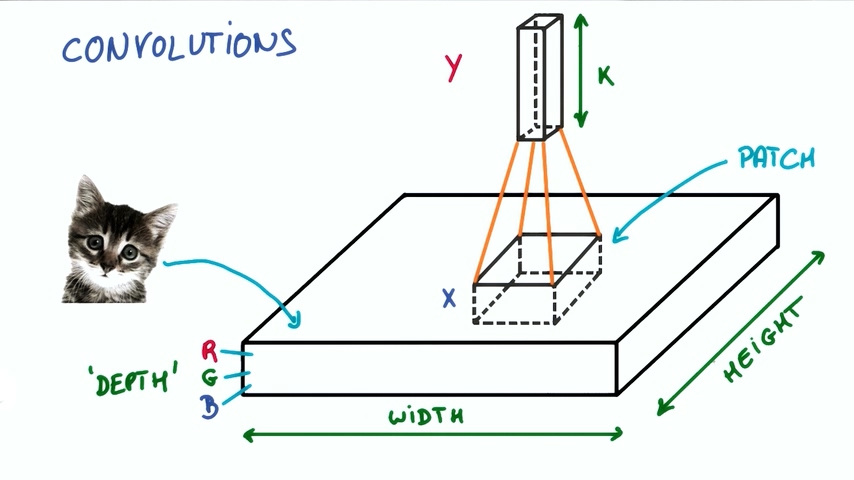
在不改变小神经网络的权重情况下,我们不断滑动从图片中取出这样的小块进行计算,把输出集合起来。
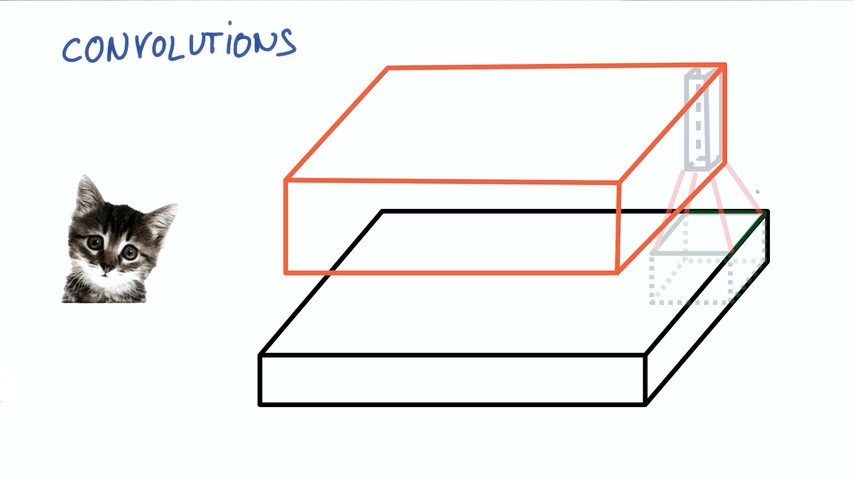
这样我们就得到了新的图像,这个图像由不同的宽度,不同的长度,最最重要的是它有不同的深度DEPTH。之前的图片的深度只有3(R/G/B),但现在的深度就有K了
这种操作就叫做卷积。如果你取的小块是和整张图片一样大,那就是普通的神经网络。正因为我们使用了比图片更小的块,我们的权重数量大大降低,而且我们在不同的块之间共享相同的权重。卷积网络是深度神经网络的基础,我们将使用数层卷积而不是数层的矩阵相乘。
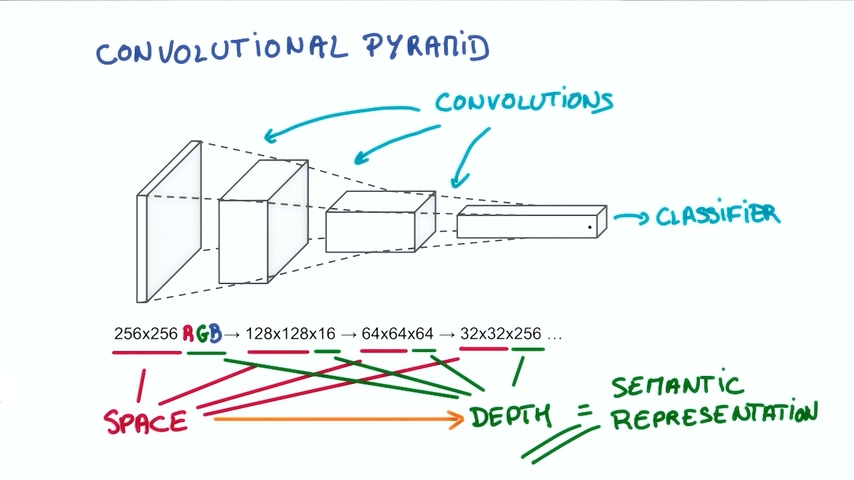
总体的思想是使得神经网络称为一个金字塔形状,金字塔底部是一个DEPTH很小,但长宽很大的图片。通过卷积逐渐挤压空间的维度,同时不断增加深度,使得我们的深度信息可以表达出复杂的语义。然后我们可以在金字塔的顶端实现一个分类器,所有的信息都逐渐被压缩成一个标识,只留下把图片映射到不同类别的信息。
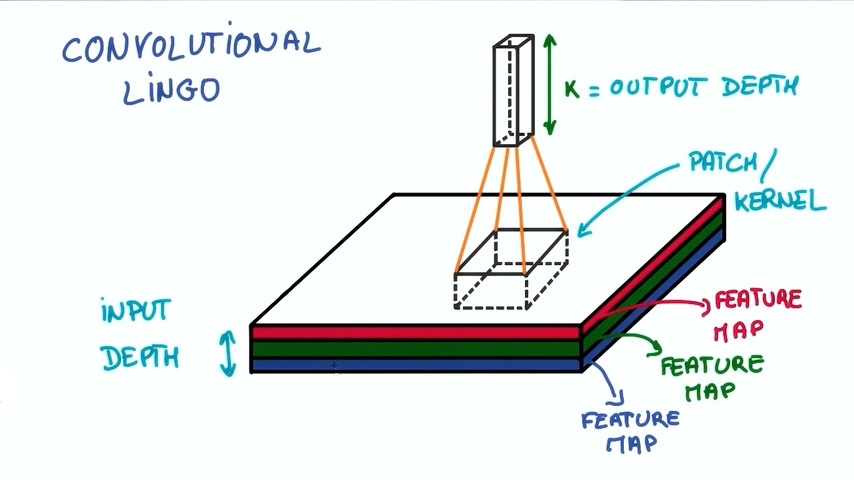
卷积神经网络Lingo
如果我们要实现卷积神经网络就要正确实现很多细节。我们已经解除了块(PATCH)和深度(DEPTH)的概念,块有时候也会成为Kernels(核),每一层深度成为特征图(feature map),例如我们图片中的RGB,我们从3个feature map映射到了k个feature map。
另外的概念是步幅Stride,它是我们的移动滤波器平移的像素数量。步幅为1时,得到的尺寸差不多和输入相同。
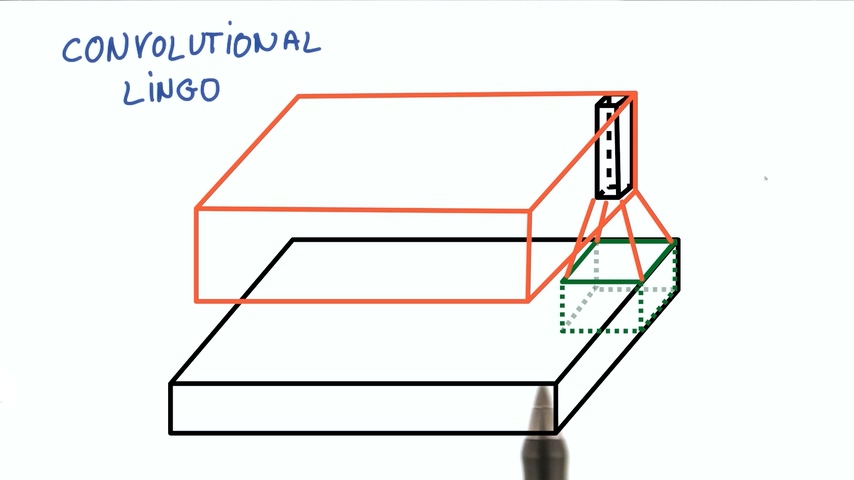
步幅为2时意味着变为差不多一半的尺寸。
这个尺寸还要看一下我们怎么处理边界。
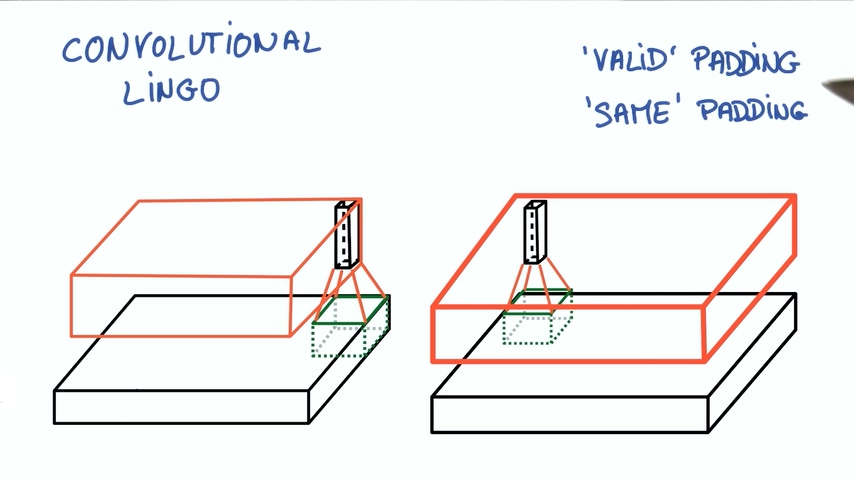
如果我们从不越过边界,这称为有效填充。
如果我们越过边界并且用0填充,这样我们会得到输入相同大小的输出,这称为相同填充

发表评论
Want to join the discussion?Feel free to contribute!