28_动手实现TensorFlow–反向传播Backpropagation
本章节我们将实现:找出各参数对Cost的影响,弄清该如何改变参数使得Cost最小化。我们不能指望盲目改变参数值却能得到正确的结果。弄清每个参数对Cost的影响的技术是反向传播,它的本质是一个链式规则。
求导
导数可以表示某个变量如何影响另一个变量,或者说某个变量对另一个变量的变化有多敏感。
举个例子:
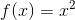
它的导数就是2x,也可以表述为:
在x这个位置f(x)的导数是2x
使用导数我们可以表示出x的变化对f(x)的影响程度。例如当x=4,f(x)的导数=8,这就表示在x=4这个位置,x变化1个单位,则f(x)会变化8个单位。
链式法则
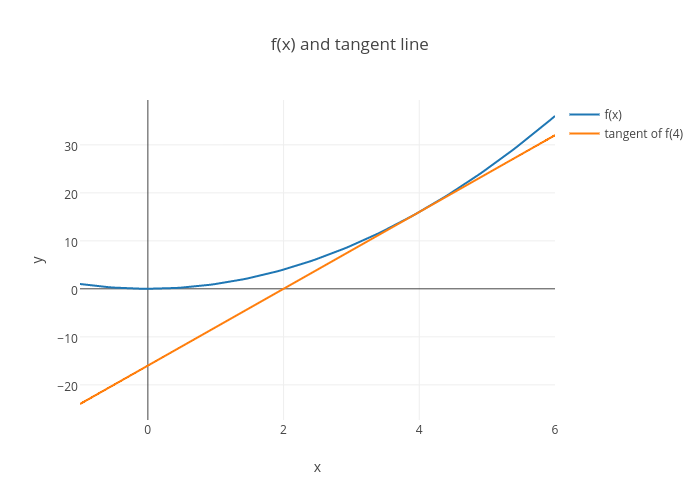
在之前的章节中我们我们只需计算网络中每个参数的Cost导数,梯度是所有这些导数的一个向量。本质上神经网络是一些方程的集合,所以计算Cost的导数就是对这些方程进行求导。
例如,对新方程求导:
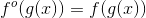
我们想计算x对整个函数的影响,也就是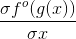 ,应用链式法则,我们得到:
,应用链式法则,我们得到:
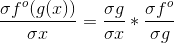
其求导过程如下:
– 求得x对g的影响
– 再求得g对fo的影响
对实际的神经网络来说:
X, y = Input(), Input()
W1, b1 = Input(), Input()
W2, b2 = Input(), Input()
l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(l2, y)
以上整个网络可以表述为MSE(Linear(Sigmoid(Linear(X, W1, b1)), W2, b2), y)。我们的目标是根据Input调整weight和biases(W1, b1, W2, b2),使得Cost最小。
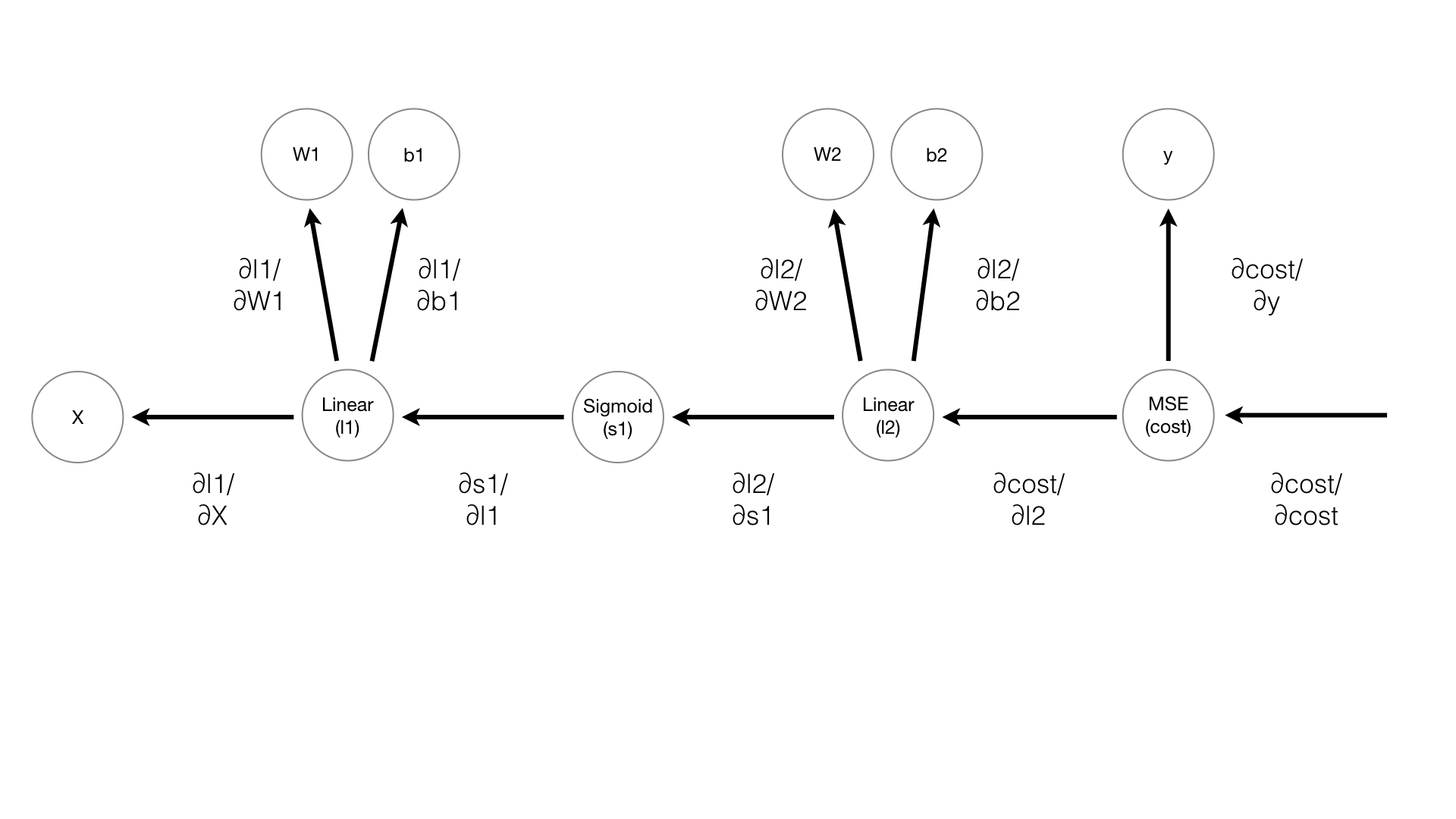
根据链式法则,以Sigmoid节点为例,对Cost和l1求导:
– ∂cost/∂l1 = (∂s1/∂l1)(∂cost/∂s1)
– 展开∂cost/∂s1:
– ∂cost/∂s1=(∂l2/∂s1)(∂cost/∂l2)
– 最终:
– ∂cost/∂l1=(∂s1/∂l1)x(∂l2/∂s1)x(∂cost/∂l2)
为了求得l1对cost的导数,我们需要得到三个值:
1. ∂s1/∂l1
2. ∂l2/∂s1
3. ∂cost/∂l2
在反向传播中我们从最后往前求导,我们首先计算∂cost/∂l2,然后计算∂l2/∂s1和∂s1/∂l1,以此类推,如果我们要计算∂s1/∂l1,则需要前面两个参数先被计算。整个过程可以参加以上的流程图。
代码实现
"""
代码来自Udacity课程,没有做更改
Implement the backward method of the Sigmoid node.
"""
import numpy as np
class Node(object):
"""
Base class for nodes in the network.
Arguments:
`inbound_nodes`: A list of nodes with edges into this node.
"""
def __init__(self, inbound_nodes=[]):
"""
Node's constructor (runs when the object is instantiated). Sets
properties that all nodes need.
"""
# A list of nodes with edges into this node.
self.inbound_nodes = inbound_nodes
# The eventual value of this node. Set by running
# the forward() method.
self.value = None
# A list of nodes that this node outputs to.
self.outbound_nodes = []
# New property! Keys are the inputs to this node and
# their values are the partials of this node with
# respect to that input.
self.gradients = {}
# Sets this node as an outbound node for all of
# this node's inputs.
for node in inbound_nodes:
node.outbound_nodes.append(self)
def forward(self):
"""
Every node that uses this class as a base class will
need to define its own `forward` method.
"""
raise NotImplementedError
def backward(self):
"""
Every node that uses this class as a base class will
need to define its own `backward` method.
"""
raise NotImplementedError
class Input(Node):
"""
A generic input into the network.
"""
def __init__(self):
# The base class constructor has to run to set all
# the properties here.
#
# The most important property on an Input is value.
# self.value is set during `topological_sort` later.
Node.__init__(self)
def forward(self):
# Do nothing because nothing is calculated.
pass
def backward(self):
# An Input node has no inputs so the gradient (derivative)
# is zero.
# The key, `self`, is reference to this object.
self.gradients = {self: 0}
# Weights and bias may be inputs, so you need to sum
# the gradient from output gradients.
for n in self.outbound_nodes:
grad_cost = n.gradients[self]
self.gradients[self] += grad_cost * 1
class Linear(Node):
"""
Represents a node that performs a linear transform.
"""
def __init__(self, X, W, b):
# The base class (Node) constructor. Weights and bias
# are treated like inbound nodes.
Node.__init__(self, [X, W, b])
def forward(self):
"""
Performs the math behind a linear transform.
"""
X = self.inbound_nodes[0].value
W = self.inbound_nodes[1].value
b = self.inbound_nodes[2].value
self.value = np.dot(X, W) + b
def backward(self):
"""
Calculates the gradient based on the output values.
"""
# Initialize a partial for each of the inbound_nodes.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Cycle through the outputs. The gradient will change depending
# on each output, so the gradients are summed over all outputs.
for n in self.outbound_nodes:
# Get the partial of the cost with respect to this node.
grad_cost = n.gradients[self]
# Set the partial of the loss with respect to this node's inputs.
self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
# Set the partial of the loss with respect to this node's weights.
self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
# Set the partial of the loss with respect to this node's bias.
self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)
class Sigmoid(Node):
"""
Represents a node that performs the sigmoid activation function.
"""
def __init__(self, node):
# The base class constructor.
Node.__init__(self, [node])
def _sigmoid(self, x):
"""
This method is separate from `forward` because it
will be used with `backward` as well.
`x`: A numpy array-like object.
"""
return 1. / (1. + np.exp(-x))
def forward(self):
"""
Perform the sigmoid function and set the value.
"""
input_value = self.inbound_nodes[0].value
self.value = self._sigmoid(input_value)
def backward(self):
"""
Calculates the gradient using the derivative of
the sigmoid function.
"""
# Initialize the gradients to 0.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Cycle through the outputs. The gradient will change depending
# on each output, so the gradients are summed over all outputs.
for n in self.outbound_nodes:
# Get the partial of the cost with respect to this node.
grad_cost = n.gradients[self]
"""
TODO: Your code goes here!
Set the gradients property to the gradients with respect to each input.
NOTE: See the Linear node and MSE node for examples.
"""
sigmoid = self.value
self.gradients[self.inbound_nodes[0]] += sigmoid*(1-sigmoid)*grad_cost
class MSE(Node):
def __init__(self, y, a):
"""
The mean squared error cost function.
Should be used as the last node for a network.
"""
# Call the base class' constructor
Node.__init__(self, [y, a])
def forward(self):
"""
Calculates the mean squared error.
"""
# NOTE: We reshape these to avoid possible matrix/vector broadcast
# errors.
#
# For example, if we subtract an array of shape (3,) from an array of shape
# (3,1) we get an array of shape(3,3) as the result when we want
# an array of shape (3,1) instead.
#
# Making both arrays (3,1) insures the result is (3,1) and does
# an elementwise subtraction as expected.
y = self.inbound_nodes[0].value.reshape(-1, 1)
a = self.inbound_nodes[1].value.reshape(-1, 1)
self.m = self.inbound_nodes[0].value.shape[0]
# Save the computed output for backward.
self.diff = y - a
self.value = np.mean(self.diff**2)
def backward(self):
"""
Calculates the gradient of the cost.
This is the final node of the network so outbound nodes
are not a concern.
"""
self.gradients[self.inbound_nodes[0]] = (2 / self.m) * self.diff
self.gradients[self.inbound_nodes[1]] = (-2 / self.m) * self.diff
def topological_sort(feed_dict):
"""
Sort the nodes in topological order using Kahn's Algorithm.
`feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.
Returns a list of sorted nodes.
"""
input_nodes = [n for n in feed_dict.keys()]
G = {}
nodes = [n for n in input_nodes]
while len(nodes) > 0:
n = nodes.pop(0)
if n not in G:
G[n] = {'in': set(), 'out': set()}
for m in n.outbound_nodes:
if m not in G:
G[m] = {'in': set(), 'out': set()}
G[n]['out'].add(m)
G[m]['in'].add(n)
nodes.append(m)
L = []
S = set(input_nodes)
while len(S) > 0:
n = S.pop()
if isinstance(n, Input):
n.value = feed_dict[n]
L.append(n)
for m in n.outbound_nodes:
G[n]['out'].remove(m)
G[m]['in'].remove(n)
# if no other incoming edges add to S
if len(G[m]['in']) == 0:
S.add(m)
return L
def forward_and_backward(graph):
"""
Performs a forward pass and a backward pass through a list of sorted Nodes.
Arguments:
`graph`: The result of calling `topological_sort`.
"""
# Forward pass
for n in graph:
n.forward()
# Backward pass
# see: https://docs.python.org/2.3/whatsnew/section-slices.html
for n in graph[::-1]:
n.backward()
测试代码:
"""
Test your network here!
No need to change this code, but feel free to tweak it
to test your network!
Make your changes to backward method of the Sigmoid class in miniflow.py
"""
import numpy as np
from miniflow import *
X, W, b = Input(), Input(), Input()
y = Input()
f = Linear(X, W, b)
a = Sigmoid(f)
cost = MSE(y, a)
X_ = np.array([[-1., -2.], [-1, -2]])
W_ = np.array([[2.], [3.]])
b_ = np.array([-3.])
y_ = np.array([1, 2])
feed_dict = {
X: X_,
y: y_,
W: W_,
b: b_,
}
graph = topological_sort(feed_dict)
forward_and_backward(graph)
# return the gradients for each Input
gradients = [t.gradients[t] for t in [X, y, W, b]]
"""
Expected output
[array([[ -3.34017280e-05, -5.01025919e-05],
[ -6.68040138e-05, -1.00206021e-04]]), array([[ 0.9999833],
[ 1.9999833]]), array([[ 5.01028709e-05],
[ 1.00205742e-04]]), array([ -5.01028709e-05])]
"""
print(gradients)
完整代码请关注我的github:
Github链接
更多文章请关注我的个人网站:
link

发表评论
Want to join the discussion?Feel free to contribute!