上节我们认识到增加隐藏层可以解决更为复杂的非线性问题，也计算出了各隐藏层节点的输入与输出值。现在问题来了，我们要怎样才能够让这种多层感知器的网络进行权重的学习呢？本节将介绍深度学习的基础：反向传播

反向传播

此前我们实现了通过梯度下降法对权重值进行更新。现在要介绍的反向传播是该方法的一个扩展。使用链式法则找到与到输入层连接到隐藏层的权重误差。

为了使隐藏层的权重也使用梯度下降法进行更新，我们需要了解误差是如何从各隐藏层节点传递到最终输出的。由于层的输出由层之间的权重确定，因此由单元产生的误差前向通过网络的权重来缩放。由于我们知道输出中的误差，我们可以使用权重向后反推到隐藏层的误差。

举个例子：在输出层，我们可以计算到误差与每个输出单元k有关。接着隐藏层的各单元j误差是输出误差被隐藏层和输出层之间的权重缩放。

然后梯度下降步骤与之前相同，使用新的误差：

Wij是输入层与隐藏层之间的权重，Xi是输入值。这种形式适用于许多层。权重变化步长等于步长大小乘以层的输出误差乘以该层输入值。

输出误差δoutput通过最高层向后传播误差。Vin是每一层的输入，例如隐藏层的激活函数输出到输出层的输入。

反向传播实例

假设现有两个输入值，一个隐藏层单元，一个输出单元，每个单元都使用sigmoid函数作为激活函数。下面的这张图解释了这个网络：

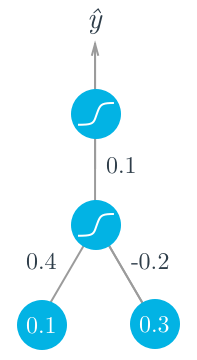
假设我们试图匹配一些数据，使得目标输出y=1.我们从前向传播开始，先计算输入到隐藏层节点：

h=0.1×0.4−0.2×0.3=−0.02
计算隐藏层的输出：

a=f(h)=sigmoid(−0.02)=0.495.

使用这个输出作为输出层的输入，最终网络输出：

y^=f(W⋅a)=sigmoid(0.1×0.495)=0.512.

得到了网络的输出，我们可以开始反向计算每一层权重的变化了：
有sigmoid函数反推得出：

f'(W⋅a)=f(W⋅a)(1−f(W⋅a))

输出的误差就是：

δ^o=(y-y^)f'(W.a)=(1−0.512)×0.512×(1−0.512)=0.12

现在我们用反向传播计算隐藏层的误差。在这里我们通过权重W对隐藏层的误差进行了缩放。

现在我们得到了误差，我们可以计算梯度下降值。

然后计算隐藏层的梯度下降值：

这个例子中由于sigmoid函数最大的微分值是0.25，所以输出层的误差被减小了至少75%，而隐藏层的误差被缩小了至少93.75%。如果有很多层，sigmoid函数将快速的使靠近输入层的权重下降到非常小的值。这就是已知的梯度消失问题。在后续的章节中我们会引入更多的激活函数，以解决这个问题。

numpy实现反向传播

import numpy as np


def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))


x = np.array([0.5, 0.1, -0.2])
target = 0.6
learnrate = 0.5

weights_input_hidden = np.array([[0.5, -0.6],
                                 [0.1, -0.2],
                                 [0.1, 0.7]])

weights_hidden_output = np.array([0.1, -0.3])

## Forward pass
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)

output_layer_in = np.dot(hidden_layer_output, weights_hidden_output)
output = sigmoid(output_layer_in)

## Backwards pass
## TODO: Calculate error
error = target - output

# TODO: Calculate error gradient for output layer
del_err_output = error * output * (1 - output)

# TODO: Calculate error gradient for hidden layer
del_err_hidden = np.dot(del_err_output, weights_hidden_output) * \
                 hidden_layer_output * (1 - hidden_layer_output)

# TODO: Calculate change in weights for hidden layer to output layer
delta_w_h_o = learnrate * del_err_output * hidden_layer_output

# TODO: Calculate change in weights for input layer to hidden layer
delta_w_i_h = learnrate * del_err_hidden * x[:, None]

print('Change in weights for hidden layer to output layer:')
print(delta_w_h_o)
print('Change in weights for input layer to hidden layer:')
print(delta_w_i_h)

将反向传播用于解决录取预测问题

数据处理与上一节相同，主要修改神经网络学习部分

np.random.seed(21)

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))


# Hyperparameters
n_hidden = 2  # number of hidden units
epochs = 900
learnrate = 0.005

n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights_input_hidden = np.random.normal(scale=1 / n_features ** .5,
                                        size=(n_features, n_hidden))
weights_hidden_output = np.random.normal(scale=1 / n_features ** .5,
                                         size=n_hidden)

for e in range(epochs):
    del_w_input_hidden = np.zeros(weights_input_hidden.shape)
    del_w_hidden_output = np.zeros(weights_hidden_output.shape)
    for x, y in zip(features.values, targets):
        ## Forward pass ##
        # TODO: Calculate the output
        hidden_input = np.dot(x, weights_input_hidden)
        hidden_output = sigmoid(hidden_input)

        output = sigmoid(np.dot(hidden_output,
                                weights_hidden_output))

        ## Backward pass ##
        # TODO: Calculate the error
        error = y - output

        # TODO: Calculate error gradient in output unit
        output_error = error * output * (1 - output)

        # TODO: propagate errors to hidden layer
        hidden_error = np.dot(output_error, weights_hidden_output) * \
                       hidden_output * (1 - hidden_output)

        # TODO: Update the change in weights
        del_w_hidden_output += output_error * hidden_output
        del_w_input_hidden += hidden_error * x[:, None]

    # TODO: Update weights
    weights_input_hidden += learnrate * del_w_input_hidden / n_records
    weights_hidden_output += learnrate * del_w_hidden_output / n_records

    # Printing out the mean square error on the training set
    if e % (epochs / 10) == 0:
        hidden_output = sigmoid(np.dot(x, weights_input_hidden))
        out = sigmoid(np.dot(hidden_output,
                             weights_hidden_output))
        loss = np.mean((out - targets) ** 2)

        if last_loss and last_loss < loss:
            print("Train loss: ", loss, "  WARNING - Loss Increasing")
        else:
            print("Train loss: ", loss)
        last_loss = loss

# Calculate accuracy on test data
hidden = sigmoid(np.dot(features_test, weights_input_hidden))
out = sigmoid(np.dot(hidden, weights_hidden_output))
predictions = out > 0.5
print(out)
print(predictions)
print(targets_test)
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))

测试结果：