05_车道线识别–Hough变换基础
前面的章节中我们在图像上画出了符合阈值的点,看起来已经覆盖了我们所需要的车道线,然而在处理时仍然是不够的,因为它们是离散的点,而我们真正的目标是确认我们获取到的这些离散的点是否是在一条线上,即我们所关心的车道线。本文我们将介绍Hough变换的基本原理以及引申出的一些知识点。
Hough变换
霍夫变换(Hough)是一个非常重要的检测间断点边界形状的方法。它通过将图像坐标空间变换到参数空间,来实现直线与曲线的拟合。请注意我们之前将图像看作是x-y坐标轴上的数字,我们将Hough变换的空间称之为Hough空间,区别于我们的图像空间(x-y坐标系)。
图像空间与Hough空间之间的转换
在图像空间,我们将一条直线描述为:
而图像中有很多个点,图像可以视为很多很多直线的集合。如果我们把这些直线的m/b都记录下来,用一个横坐标为m,纵坐标为b的空间来表示,我们将能够很好地将这些直线归类,每条直线的m/b是固定的,一条直线在这个空间中就是一个点,这就是Hough空间。
直线的Hough变换
试想有图像空间中有两条平行线,如下图所示
那么,请思考这两条直线在Hough空间中应该是什么样的呢?
答案:
由于平行线的斜率是一样的,那么这两条直线的m参数是一样的,b参数有差别,所以在Hough空间中应该是同一个m参数不同b参数的两个点,如下图所示:
单点的Hough变换
我们现在知道图像空间中的一条直线在Hough空间中是一个点,那么,问题来了,图像空间中的一个点在Hough空间中又该怎么表示呢?
答案:
我们知道,Hough空间中的m和b是来源于图像空间中的直线表达方式:Y=mX+b,图像空间中已知一个点X0,Y0,求m和b直接将公式反过来不就可以了吗?于是我们得到:b=Y0-mX0因此,在Hough空间中应该对应的是一条直线,斜率为-X0
两个点的Hough变换
很有趣吧?两个点在Hough空间上会是怎么样的呢?
答案:
我们知道一个点对应Hough空间中一条直线,两个点当然是两条直线咯。可是这两条直线是怎么样的呢?是平行线吗?当然不是。因为两点确定一条直线,当图像空间中的这两个点在同一条直线上的时候对应的m和b都是一样的。那么图像空间中的两个点在Hough空间中就会是两条相交的直线。
Hough空间到图像空间的变换
上面我们知道Hough空间中两条交叉的直线代表图像空间中的两个点,那么在Hough空间中的这个交叉点对应到图像空间中应该是将两个点连起来的直线。
大问题:图像空间中很多点的Hough变换
我们已经知道图像空间中每个点在Hough变换中表现出一条直线,并且任意两个点之间在Hough空间中的直线必定会相交。由此我们在Hough空间中会得到很多条直线,以及很多个交点。
假如图像空间中的这些点在散步在某一条直线周围,那这些点转换到Hough空间后得出的直线相交点就会聚集在一个区域内,这可是一大利器,我们终于可以用Hough变换去确定这些孤立的点是不是在车道线上了!
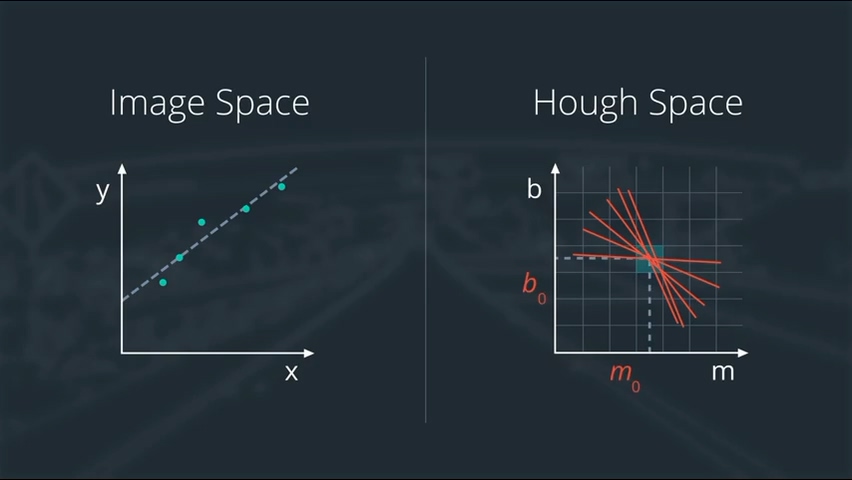
m和b的弊端
别急着高兴,我们似乎遇到点麻烦:使用直角坐标表示直线,当直线为一条垂直直线或者接近垂直直线时,该直线的斜率为无限大或者接近无限大,从而无法在Hough空间上用m和b表示出来。为了解决这个问题,可以采用极坐标。
引入极坐标表示方法
在图像空间中,还有另外一种方法可以表示直线:
其中,ρ代表直线到原点的垂直距离,θ代表x轴到直线垂线的角度,取值范围为±90∘,如图所示

由此我们可以确定,Hough空间不用m和b表示,我们仍然可以用\theta和P表示嘛
重复m和b的故事
一个点在Hough空间中怎么用\theta和P表示呢?
那么这不就是一条正弦曲线了么?同样的,两个点就是两条正弦曲线,并且有一个交点。以此类推。
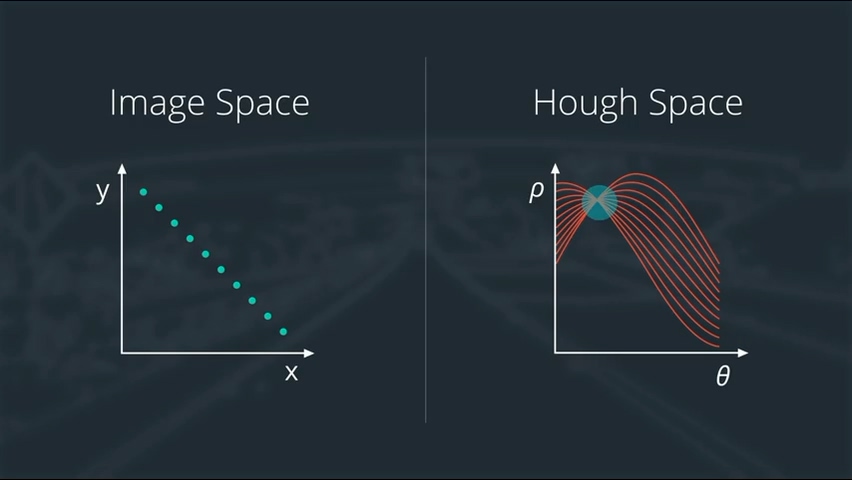
思考一下:
如下图的图像空间在Hough空间中怎么用 \theta 和P表示?
没错,这里面可以画出4条可以涵盖尽可能多点的直线,因此在Hough空间中应该有4个较为稠密的交叉点:
其他
更多知识请访问我的网站vivi实验室

发表评论
Want to join the discussion?Feel free to contribute!