经过上一节课的完善，我们的MiniFlow已经可以像神经网络一样接受输入数据，产生输出数据了。但是神经网络还有一个重要特征就是可以通过训练逐渐提升精度。但我们只有一个Add节点，这是无法提升精度的。为了达到提升精度的目的，我们引入一个比Add节点更有用的节点类型：线性节点。

线性节点

在“神经网络”章节中我们曾经提到过，一个简单的神经网络依赖于：
– 输入input x（向量）
– 权重weight w（向量）
– 偏置bias b（常量）

O是输出。
这是最简单的线性节点，我们知道神经网络是可以通过反向传播更新权重值的，当前我们先不进行处理。

class Linear(Node):
    def __init__(self, inputs, weights, bias):
        Node.__init__(self, [inputs, weights, bias])

        # NOTE: The weights and bias properties here are not
        # numbers, but rather references to other nodes.
        # The weight and bias values are stored within the
        # respective nodes.

    def forward(self):
        """
        Set self.value to the value of the linear function output.

        Your code goes here!
        """
        v = 0
        for i in range(len(self.inbound_nodes[0].value)):
            v += self.inbound_nodes[0].value[i]*self.inbound_nodes[1].value[i]
        self.value = v + self.inbound_nodes[2].value
        pass

线性变换

线性代数很好地反映了在图中层之间转换数值的想法。 事实上，变换的概念正是层应该做的 — 它将输入转换为多维的输出。
请注意层之间的连接：

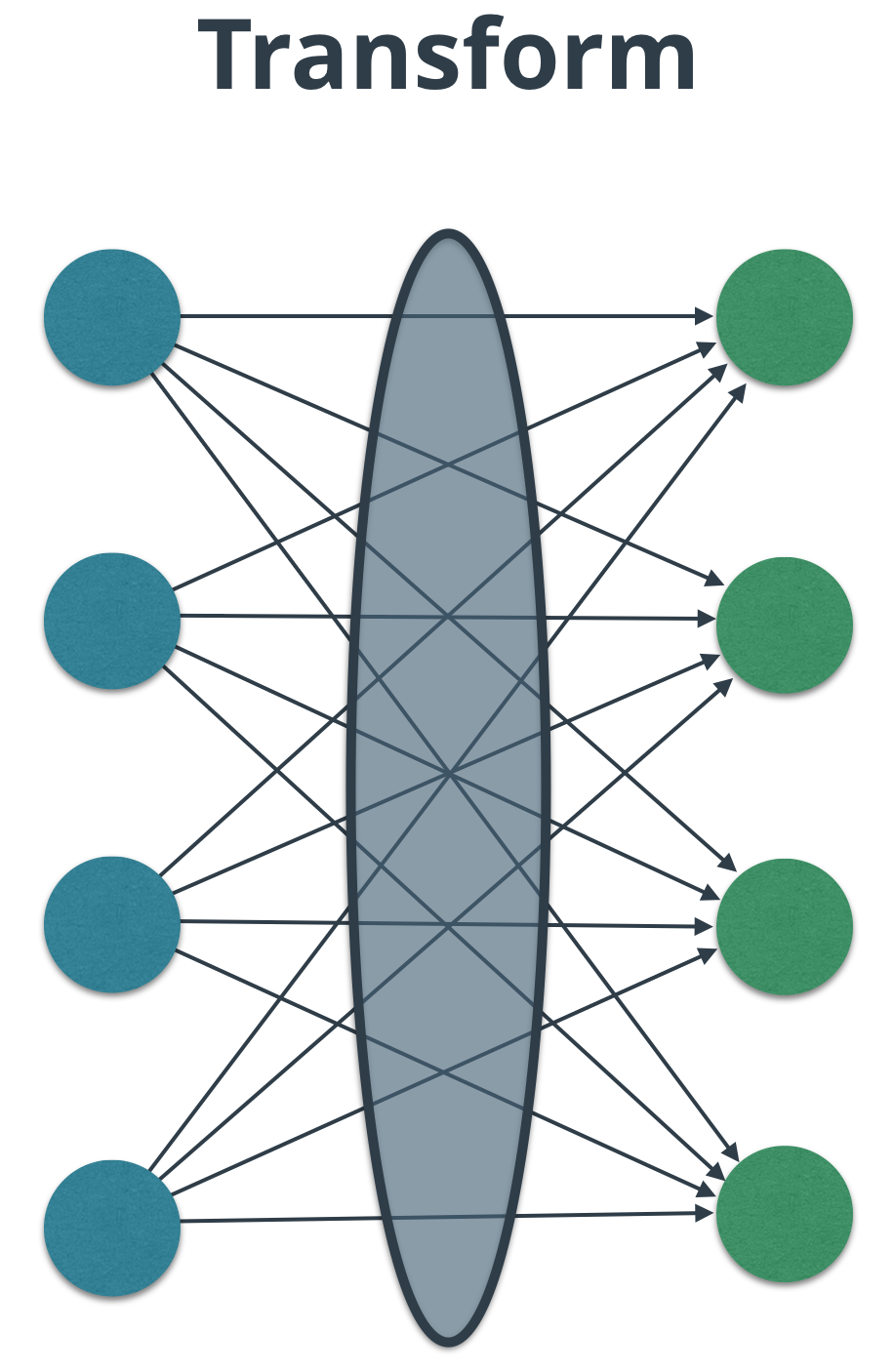
由于权重、输入经常是矩阵形式，所以我们的Linear函数也应该可以处理矩阵运算：

class Linear(Node):
    def __init__(self, X, W, b):
        # Notice the ordering of the input nodes passed to the
        # Node constructor.
        Node.__init__(self, [X, W, b])

    def forward(self):
        """
        Set the value of this node to the linear transform output.

        Your code goes here!
        """
        inputs = self.inbound_nodes[0].value
        weights = self.inbound_nodes[1].value
        bias = self.inbound_nodes[2].value
        self.value = 0
        self.value += np.dot(inputs, weights)+bias

在这里我们用了numpy的点乘dot()以及numpy的矩阵相加，感兴趣的小伙伴请参考numpy的文档

传入数据

在nn.py中我们传入数据到miniflow：

mport numpy as np
from miniflow import *

X, W, b = Input(), Input(), Input()

f = Linear(X, W, b)

X_ = np.array([[-1., -2.], [-1, -2]])
W_ = np.array([[2., -3], [2., -3]])
b_ = np.array([-3., -5])

feed_dict = {X: X_, W: W_, b: b_}

graph = topological_sort(feed_dict)
output = forward_pass(f, graph)

"""
Output should be:
[[-9., 4.],
[-9., 4.]]
"""
print(output)

完整代码链接详见github：https://github.com/vvchenvv/Self_Driving_Tutorial/tree/master/Class1/24_Linear_Transform

更多内容请关注我的网站